Ques.91. The DC output power across a load of R ohms in a half-wave rectifier with a current flowing of peak value Im is
- (Im2R)/π
- (Im/π)2 R✓
- (Im2R)/2π
- (Im/2π)2 R
Practically DC source provides an absolutely constant voltage which means that it is not alternating in nature. Hence the average value of DC voltage or current is equal to the Peak or maximum value of DC voltage or current. The dc value of a half-wave rectified signal is the same as the average value. If you measure a signal with a dc voltmeter, the reading will equal the average value and it is given as Idc = Im/π Power = I2mR PDC = (Im/π)2 R
Ques.92. The common emitter transistor circuit has
- High Gain✓
- Low Gain
- Negligible Gain
- No Gain
Out of the three transistor connections, the common-emitter circuit is the most efficient. It is used in about 90 to 95 percent of all-transistor applications. The main reasons for this are : High current gain In a common emitter connection, Ic is the output current and IB is the input current. The collector current here is expressed as: Ic = βIB + ICEO As the value of β is very large, therefore, the output current IC is much more than the input current IB. This increases the current gain effectively. The current gain of CE arrangement ranges from 20 to High Voltage and Power Gain As we have seen above, the CE arrangement has a high current gain. This in turn, increases the voltage and power gain of the CE circuit. In comparison to CB and CC circuits, the common emitter connection has the highest voltage and power gain. For this reason, the CE transistor connection is often used for amplifying purposes
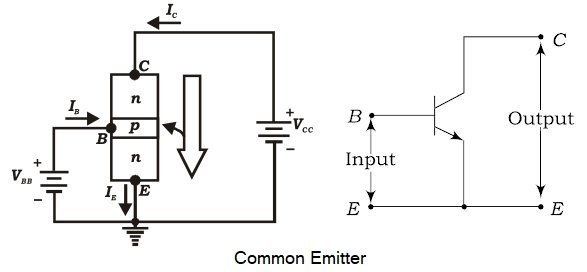
Where β = Current Gain
ICEO = Collector-Emitter current
500.
Ques.93. The circuit that provides the best stabilization of operating point is
- Base resistor Bias
- Collector Feedback Bias
- Potential divider bias✓
- None of these
The circuit that provides the best stabilization of operating point is Potential divider bias. The potential divider or self-biasing for an NPN transistor of a common emitter configuration is shown in Fig. This biasing circuit consists of two resistors R1 and R2 connected across the supply voltage VCC and provides the necessary biasing. Whereas, a resistor connected in the emitter circuit RE provides thermal stability and improves stability factor. Since the resistor R1 and R2 form the potential divider hence the name potential divider biasing. This biasing is the most widely used method of providing biasing and stabilization to transistors since the operating point, in this case, can be made almost independent of β (collector Current). We know that a bipolar junction transistor can operate in one of three regions – cutoff, saturation, and active. When we want to use the transistor as a switch (i.e. in digital circuits) we use the transistor in cutoff and saturation. But, when we want to use the transistor as an amplifier, we use it in the active region. When the transistor is biased in the active region, a small signal applied to the input terminal appears as a larger signal at the output terminal. This is what is called amplification. To bias in the active region, we must assign a fixed value to two quantities – Vce and Ic – the transistor output voltage and output current. Assigning these fixed values is called setting the transistor Q point or bias point. In order for the amplifier to amplify properly, it is important that the steady-state (or DC) values of Vce and Ic do not change. What this means is that when there is no input to the transistor, the transistor output voltage and current will be DC, and they should remain constant. However, the flow of current Ic produces heat. Because of this heat, our Q point begins to shift. So, we need a mechanism that will prevent the change in the Q point values when the temperature rises. In other words, we want a stable Q point. Here again, we look at the KVL equations: VCC – ICRC – Vce – IeRe = 0 Vcc – I1R1 – Vbe – IeRe = 0 The KCL expression for the transistor is: Ie = Ic + Ib Now, when the temperature rises, Ic increases. From the KCL expression, we see that this causes Ie to increase. When Ie increases, the drop IeRe will also increase. Now, look at this KVL expression: Vcc – I1R1 – Vbe – IeRe = 0 Here, Vcc is constant and I1R1 is constant. These values do not change when the temperature rises. So, if IeRe increases, then for the equation to remain valid, Vbe must decrease. From transistor action, if Vbe decreases, then Ic will also decrease. So, again we see that when heat causes Ic to increase, a series of events occur that causes Ic to decrease. When we evaluate the stability expression for this voltage divider circuit, we will find that theoretically, this circuit gives a stability factor of almost 1. A low stability factor tells us that the bias circuit is very stable. Remember, that for the collector feedback bias, this stability value was nominally 50 to 100. Hence potential-divider bias offers a very small variation of collector current or, in other words, a coot stability factor, and hence is the best method.
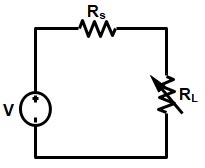
Ques.94. In an amplifier, the maximum power transfer to the load resistance should be
- As small as possible
- As large as possible
- Equal to the value of the input resistance of the amplifier✓
- Equal to the value of the output increases
Maximum Power Transfer Theorem can be stated as – A resistive load is connected to a DC network, receives maximum power when the load resistance is equal to the internal resistance known as (Thevenin’s equivalent resistance). The maximum power transfer theorem is applied to both the DC and AC circuits. The only difference is that in an AC circuit the resistance is substituted by the impedance. Let V be the voltage source, Rs be the internal resistance of the source and RL be the load resistance or the Thevenin resistance. $\begin{array}{l}P = {I^2}{R_L} = \dfrac{{{V^{_2}}{R_L}}}{{{{\left( {{R_s} + {R_L}} \right)}^2}}} – – – – – – (1)\\\\{\text{For Maximum Power to Transfer}}\\\\\dfrac{{dP}}{{d{R_L}}} = 0\\\\ = {V^2}\left[ {\dfrac{{\left( {{R_s} + {R_L}} \right) – 2{R_L}\left( {{R_s} + {R_L}} \right)}}{{{{\left( {{R_s} + {R_L}} \right)}^4}}}} \right]\\\\\therefore {R_s} = {R_L}\\\\{\text{Putting }}{{\rm{R}}_{\rm{L}}}{\rm{ = }}{{\rm{R}}_{\rm{s}}}{\text{ in eqn 1}}\\\\{P_{\max }} = \dfrac{{{V^2}}}{{4{R_L}}}\end{array}$ Maximum Power Transfer Theorem
Ques.95. In synchronous motor the rotor copper losses, are met by
- Armature input
- D.C source✓
- Motor input
- Supply lines
The synchronous motor consist of two parts: Stator: Stator is the armature winding. It consists of three-phase star or delta-connected winding and is excited by 3 phase A.C supply. Rotor: Rotor is a field winding. The field winding is excited by the separate D.C supply through the slip ring.
(i)The net mechanical output from the shaft
(ii) Copper losses in the armature winding
(iii) Friction and the armature core losses
Ques.96. The change of D.C. excitation of a synchronous motor changes
- Motor Speed
- Applied voltage of the Motor
- Power Factor✓
- All Options are correct
The change of D.C. excitation of a synchronous motor changes Power Factor. In synchronous Motor the changes in the dc field excitation do not affect the motor speed. However, such changes do alter the power factor of a synchronous motor. If all of the resistance of the rheostat is inserted in the field circuit, the field current drops below its normal value. A poor lagging power factor results. If the dc field is weak, the three-phase ac circuit to the stator supplies a magnetizing current to strengthen the field or the lagging reactive power will be drawn from the A.C source to aid magnetization. This magnetizing component lags the voltage by 90 electrical degrees. The magnetizing current becomes a large part of the total current input. This gives rise to a low lagging power factor. If a weak dc field is strengthened, the three-phase ac circuit to the stator supplies less magnetizing current and the leading current is drawn from the ac source to compensate (oppose) the magnetization. Because this current component becomes a smaller part of the total current input to the stator winding, the power factor increases. The field strength can be increased until the power factor is unity or 100%. When the power factor reaches unity, the three-phase ac circuit supplies energy current only. The dc field circuit supplies all of the current required to magnetize the motor. The amount of dc field excitation required to obtain a unity power factor is called normal field excitation. The magnetic field of the rotor can be strengthened still more by increasing the dc field current above the normal excitation value. The power factor in this case decreases. The circuit feeding the stator winding delivers a demagnetizing component of current. This current opposes the rotor field and weakens it until it returns to the normal magnetic strength. Hence Higher PF means the low requirement of MMF for energy transfer, hence low magnetizing current requirement. The synchronous machine has separate DC excitation which reduces the machine’s excitation dependency on the main supply, hence better PF. whereas the Induction motor has no such provisions, hence low Power factor.
Ques.97. The advantage of a stationary armature of a synchronous machine is
- Reducing the number of slip rings on the rotor
- The difficulty of providing high voltage insulation on the rotor
- The armature is associated with large power as compared to the field circuits
- All options are correct✓
Explanation:- FIELD AND ARMATURE CONFIGURATIONS There are two arrangements of fields and armatures: In large alternators, the rotating field arrangement is usually forward due to the following advantages. Hence in almost all of the alternators, the armature is housed in the stator while the dc field system is placed in the rotor.
ADVANTAGES OF ROTATING FIELD IN AN ALTERNATOR
Ques.98. In which of the following motors the stator and rotor fields rotate simultaneously
- Reluctance motor
- Universal Motor
- D.C Motor
- Synchronous Motor✓
The synchronous motor is a truly constant speed motor. This is the specialty of this motor. To develop a steady torque, its rotor must be rotating at synchronous speed, Ns. This is the major defect of synchronous motors. Either it runs at synchronous speed, or it does not run at all. The stator field rotates at synchronous speed due to the three-phase currents supplied to its windings. In order to develop a continuous unidirectional torque, it is necessary that the stator and rotor poles do not move with respect to each other. This is possible only if the rotor also rotates at synchronous speed. Therefore Magnetic Locking between the poles is necessary to do so. The concept of Magnetic Locking So for rotating magnetic field Where f = supply frequency At zero speed or at any other speed lower than synchronous speed, the rotor poles rotate slower than the stator field. Therefore, in one cycle of rotation of the stator field, the N-pole of the rotor is for some time nearer to the N pole of the stator and for some other time nearer to the S-pole of the stator. As a result, the torque developed is for some time clockwise and for some other time anticlockwise. Consequently, the average torque developed remains zero. Hence the Synchronous Motor Run is either on Synchronous Speed Or Not at all.
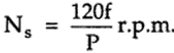
P = Number of poles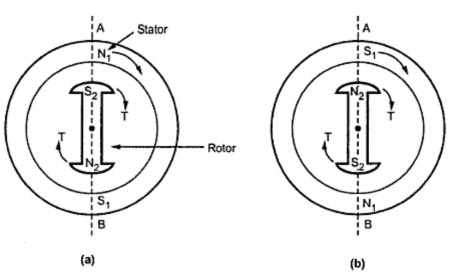
Ques.99. In a 3-phase synchronous motor, If the direction of its field current is reversed
- The winding of the motor will burn
- The motor will stop
- The motor will run in the reverse direction
- The motor continues to run in the same direction✓
In a 3-phase synchronous motor, If the direction of its field current is reversed then the motor continues to run in the same direction. The synchronous motor is a doubly excited machine with a stator and Rotor. The stator is usually excited by the three-phase supply and the rotor is excited by a DC supply in order to create a magnetic field. The three-phase supply is usually fed to the stator, the three-phase current is generated in the stator winding since it is a closed circuit. These current phases are separated by 120 degrees from each other. As a result, three-phase flux is generated which is equal in magnitude but are displaced by 120 degrees with each other. However, the rotor is excited by DC supply which usually creates poles of opposite polarity due to the positive and negative supply of dc. So the rotor is rotated by external means by using some pony Motors or induction motors so that it is interlocked with the stator field this rotates with the same speed as a stator named the synchronous speed. Interchanging the polarity during the running of the motor It should be noted that it is a very difficult procedure to change the polarity of the rotor suddenly. However, if we do so, the rotor will lose its magnetic interlocking with a stator for a second. Due to the inertia of the rotor, it will be rotating at some speed. Now the stator speed is faster than the rotor, as a result, the rotor field is again interlocked with the stator at a particular point of time during the run. Think of a magnet. It always looks for opposite polarity. So it will get interlocked at a particular point. Hence it rotates in the same direction as the stator. It neither changes its direction of rotation nor it stops All this happens within seconds that it is impossible to trace because the normal operating speed is around 1500 rpm. At that speed, it is impossible to trace this effect. Hence the direction of rotation of the synchronous motor is determined by its starting direction, as initiated by induction motor action. Thus, to reverse the direction of a 3 phase synchronous motor, it is necessary to first stop the motor and then reverse the phase sequence of the 3 phase connections at the stator. REVERSING THE CURRENT TO FIELD WINDINGS WILL NOT AFFECT THE DIRECTION OF ROTATION.
Ques.100. The maximum power developed in a synchronous motor will depend on
- The rotor excitation and supply voltage
- The rotor excitation, supply voltage and maximum value of coupling angle✓
- The supply voltage only
- The rotor excitation only
The maximum power developed in the synchronous Motor is given by the expression ${P_{\max }} = \dfrac{{{E_b}V}}{{{Z_s}}}\cos (\theta – \delta ) – \dfrac{{E_b^2}}{{{Z_s}}}Cos\theta$ Where δ = load angle θ = Internal angle V = Terminal voltage Eb = Back EMF or excitation because back EMF Eb in Synchronous Motor depends on the DC excitation only because speed is constant The power developed depends on the excitation, voltage, and coupling angle. The maximum value of θ and hence δ is 90°. An increase in the excitation results in an increase of Pmax. Consequently, the load angle decreases for a given power developed. The overload capacity of the motor increases with an increase in excitation and the machine becomes more stable. For all values of V and Eb, this limiting value of δ is the same but maximum torque will be proportional to the maximum power developed If the resistance of the armature is negligible, then Z ≅ Xs, θ = 90° ∴ Cosθ = 0 Therefore the power develop is given by ${P_{\max }} = \dfrac{{{E_b}V}}{{{X_s}}}\sin \delta$ Hence the power develop will me maximum when δ is 90°.
For SSC JE 2018 SET-1 Electrical paper with complete solution Click Here
For SSC JE 2018 SET-2 Electrical paper with complete solution Click Here
For SSC JE 2018 SET-3 Electrical paper with complete solution Click Here
For SSC JE 2018 SET-4 Electrical paper with complete solution Click Here
For SSC JE 2017 Electrical paper with complete solution Click Here
For SSC JE 2015 Electrical paper with complete solution Click Here
For SSC JE 2014 (Evening shift) Electrical paper with complete solution Click Here
For SSC JE 2014 (Morning shift) Electrical paper with complete solution Click Here
For SSC JE 2013 Electrical paper with complete solution Click Here
For SSC JE 2012 Electrical paper with complete solution Click Here
For SSC JE 2011 Electrical paper with complete solution Click Here
For SSC JE 2010 Electrical paper with complete solution Click Here
For SSC JE 2009 Electrical paper with complete solution Click Here





